En este tutorial, discutiremos el álgebra vectorial y los cálculos correspondientes en Scientific Linux. Para nuestro propósito, he elegido Python como lenguaje de programación por su simplicidad y poder de cálculo. Cualquier distribución de Linux tiene por defecto un editor/compilador de Python que se invoca a través de una ventana de terminal. Repasemos algunos conceptos de álgebra vectorial.
Nota:solo vamos a trabajar en el espacio real de dos o tres dimensiones.
Álgebra vectorial
El Elemento de un espacio vectorial, desde un punto de vista matemático, se puede representar como el arreglo de un número de elementos que pertenecen a ese espacio vectorial. Más específicamente, y en un enfoque de computación numérica, se puede representar como una lista de números reales, que tiene tres características básicas:
Magnitud
El tamaño del vector y se representa con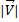 
;esta es la parte escalar de un vector. Para calcular la magnitud de un vector tenemos que realizar la siguiente fórmula:
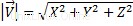
X, Y y Z son las coordenadas vectoriales.
Dirección
La dirección de un vector está dada por una línea directriz que tiene un ángulo específico para cada eje del sistema de coordenadas llamado ángulo director.
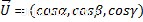
Donde alfa, beta y gamma son los ángulos directores del vector y sus cosenos son los cosenos directores, también se pueden calcular dividiendo cada coordenada vectorial por su magnitud.
Orientación
Una de las dos orientaciones posibles entre la misma dirección.
Suma algebraica vectorial
Para realizar una suma algebraica de vectores, debemos sumar las coordenadas homólogas de dos vectores, atendiendo a las mismas propiedades de la suma algebraica de números reales. Solo como sigue:
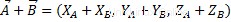Como podemos ver, el resultado es otro vector, perteneciente al mismo espacio vectorial.
Producto de un vector por un escalar
Dado un vector y un escalar, el producto vectorial por un escalar se define como el producto escalar de cada coordenada del vector:
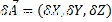
Dónde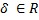 
Vector Unidad
Una aplicación directa para el vector Producto por un escalar es el vector unitario, a vector unitario es un vector normado de longitud 1.
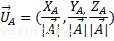
Combinación lineal
Cuando mezclamos las operaciones pasadas, suma algebraica y producto vector-escalar, obtenemos una combinación lineal, en la que el resultado es también un vector perteneciente al mismo espacio vectorial, como es:
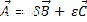
Donde el vector A es una combinación lineal de los vectores B y C.
Python en Scientific Linux 7.1
Para implementar el álgebra vectorial elegimos Python como lenguaje de cálculo. El editor de texto que elegimos es gedit y viene por defecto con la distro Scientific Linux 7.1.
Magnitud de un vector
Llamemos a gedit usando una terminal o simplemente haga clic en el ícono en la pestaña de aplicaciones:
Primero debemos trabajar con listas, ya que representan vectores y deben declararse como es:
V=[2, 2, 1]
Declaremos una variable para almacenar la magnitud y dar un valor, usamos 0.
modV=0
Ahora usamos la clase math para operar la raíz cuadrada:
import math
El cálculo de la magnitud:
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
Como podemos ver, tenemos que usar subíndice para indicar el elemento de la lista que vamos a operar, comenzando desde 0.
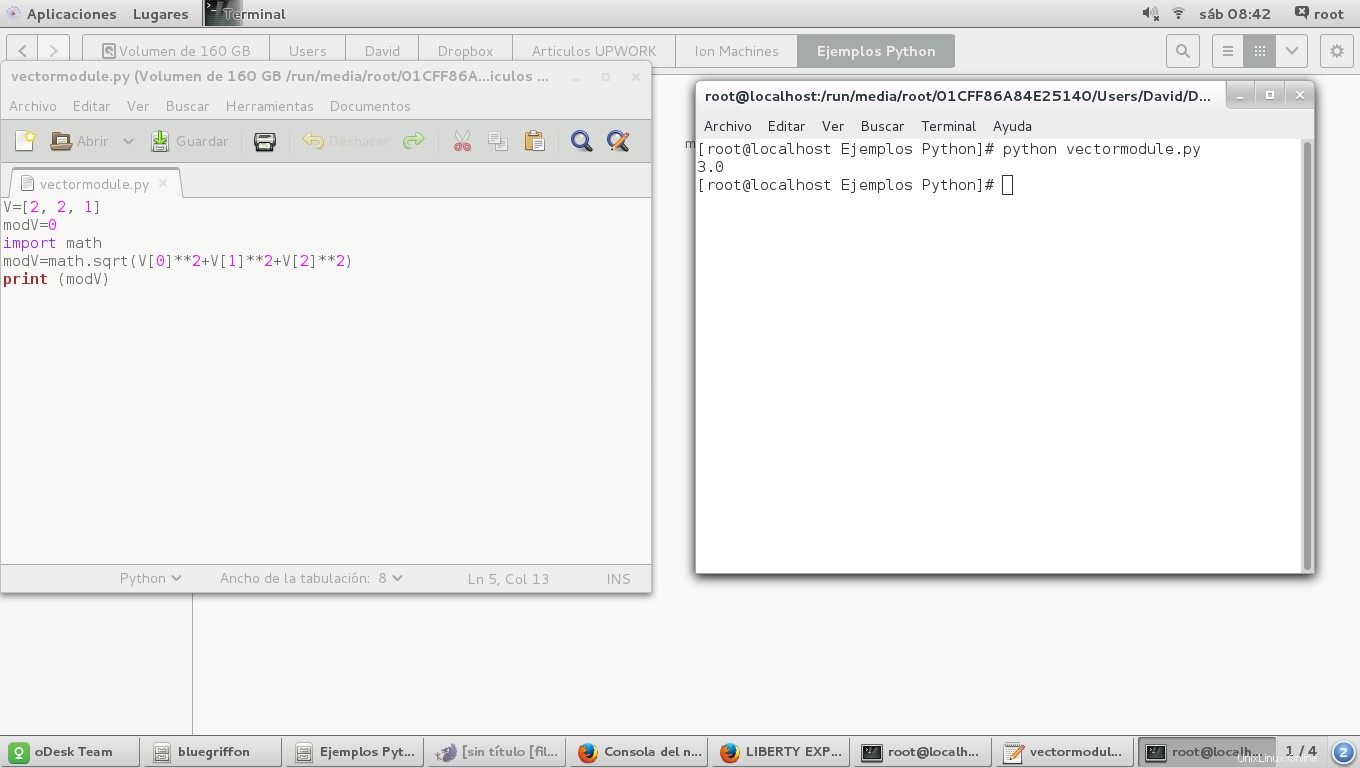
El script completo es el siguiente:
V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)
Una vez terminado, tenemos que guardar el archivo con la extensión .py y ubicar la ruta del archivo y abrir una ventana de terminal allí con el botón derecho y luego "abrir en ventana de terminal". Después tenemos que llamar al intérprete de python escribiendo:
$ python [path]/yourfilename.py
esto abrirá una ventana como esta y dará el resultado:
Otra forma de hacerlo es usando un bucle for como estos:
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)
Aquí tenemos que usar técnicas de sangría ya que el intérprete de python funciona de esa manera.
Dirección de un vector
Usa las matemáticas de la clase
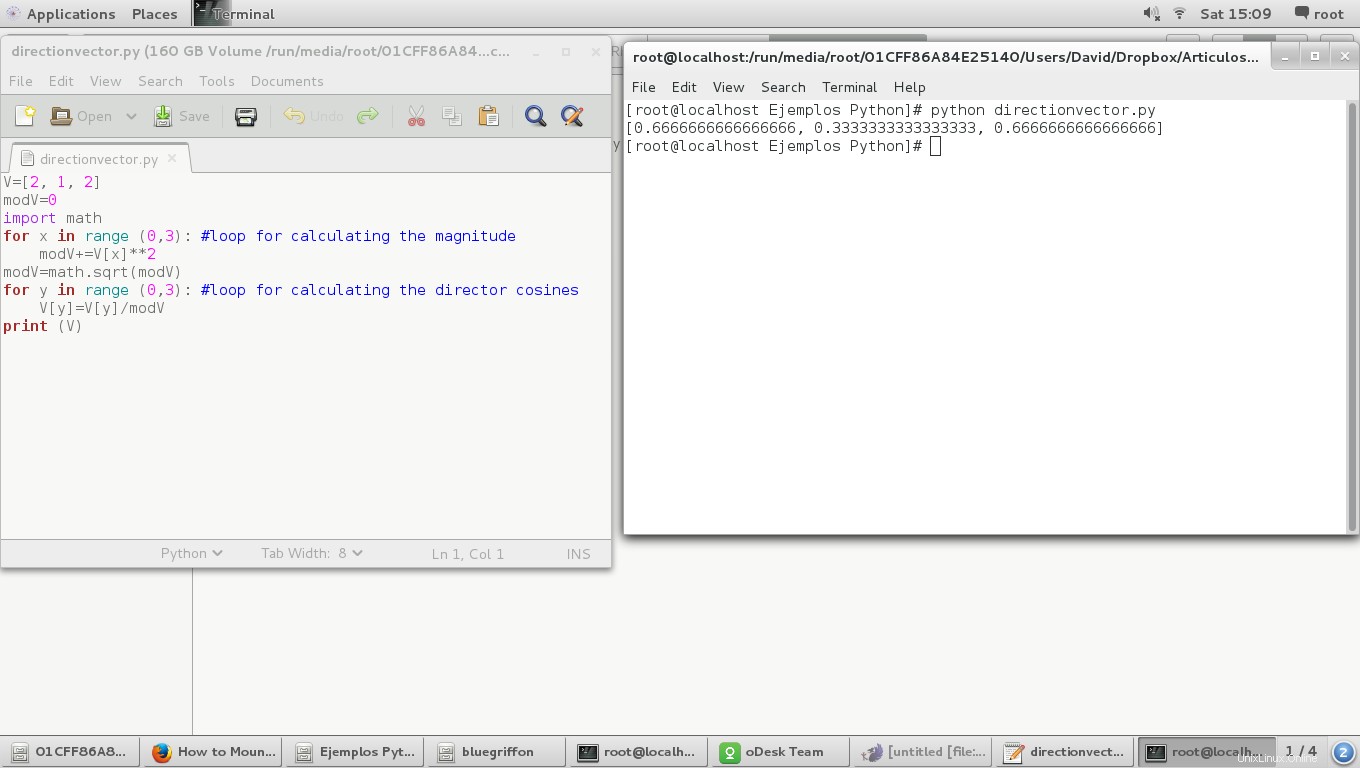
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)
El resultado es el siguiente:
Otra forma de hacerlo es usando las funciones trigonométricas de la clase de matemáticas, simplemente así:
Primero calculemos los ángulos directores:
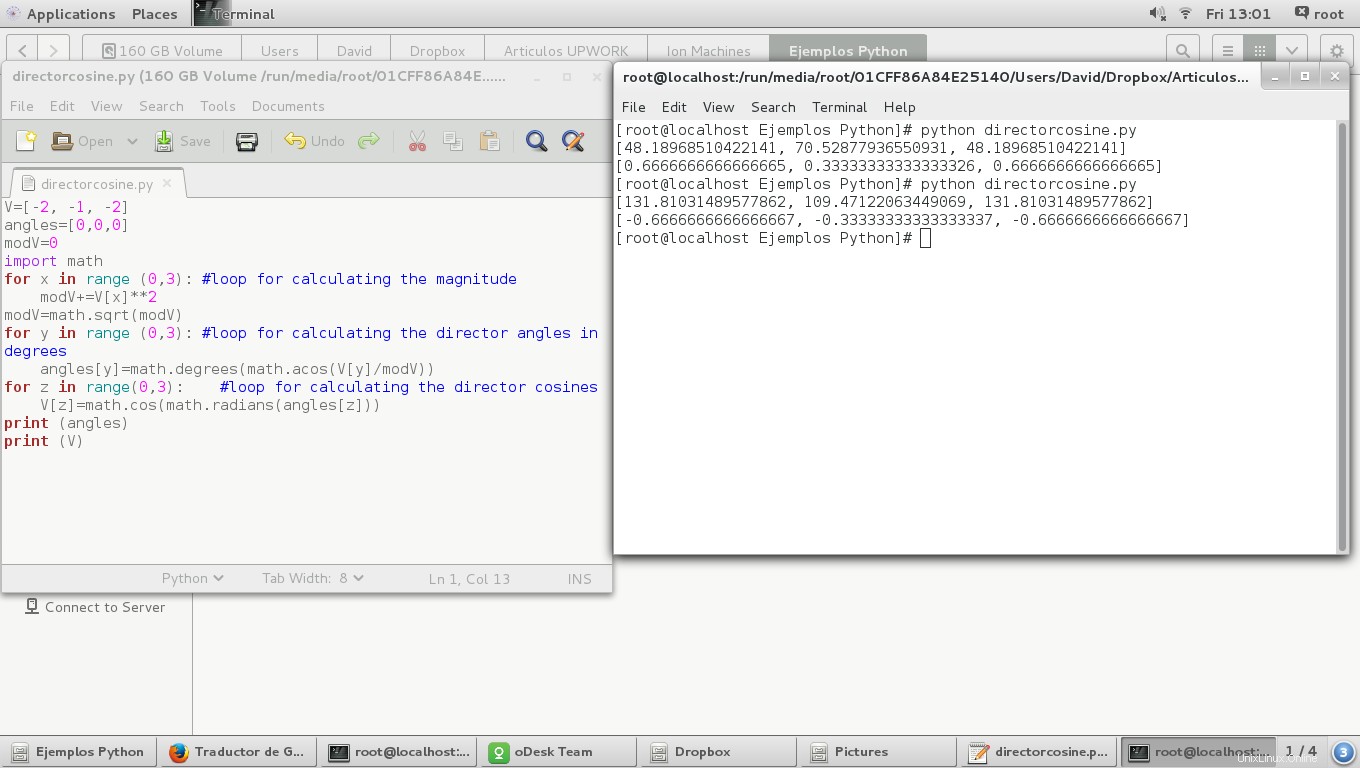
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))
Y luego calculemos los cosenos directores y los imprimamos
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
Y el resultado:
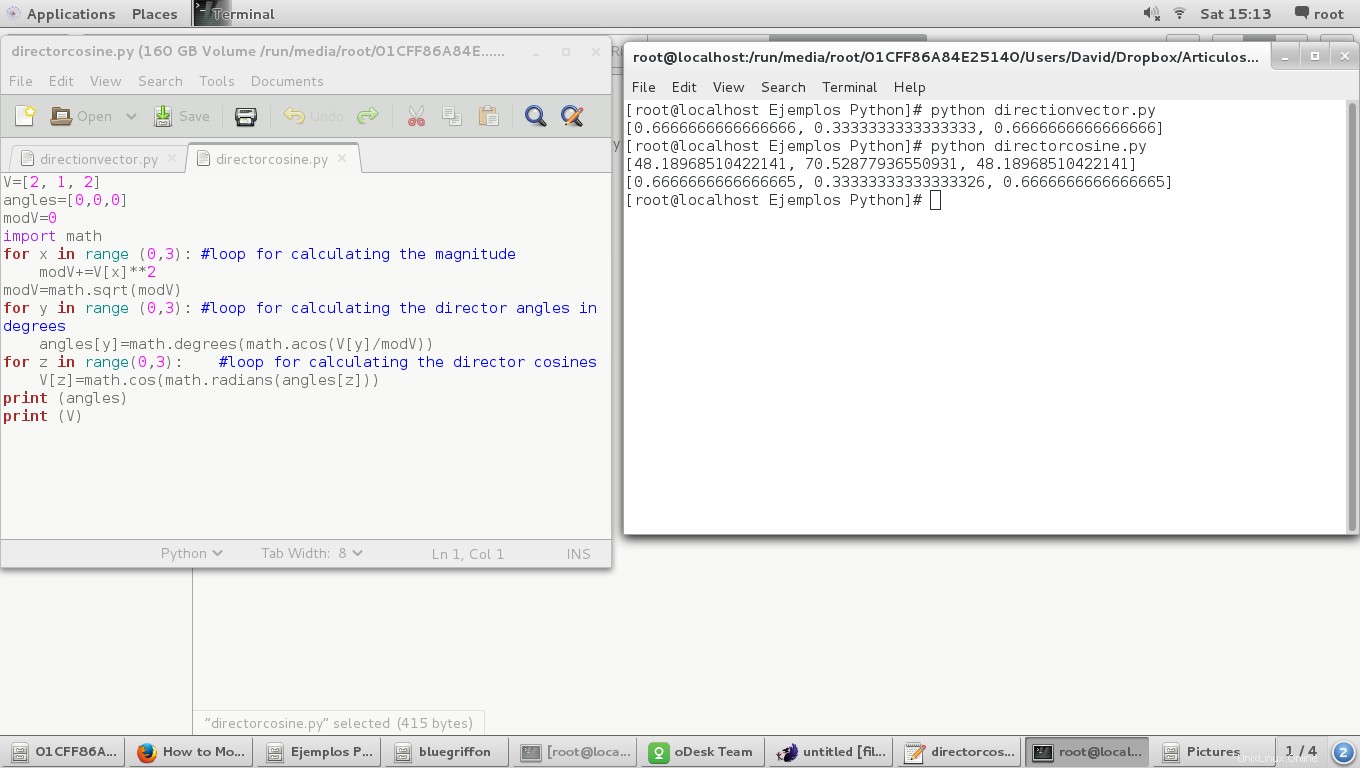
Podemos observar que los cosenos directores tienen el mismo valor
Orientación de un vector
Si cambiamos el signo de todas las coordenadas de un vector, inherentemente estamos cambiando la orientación del vector, como es:
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
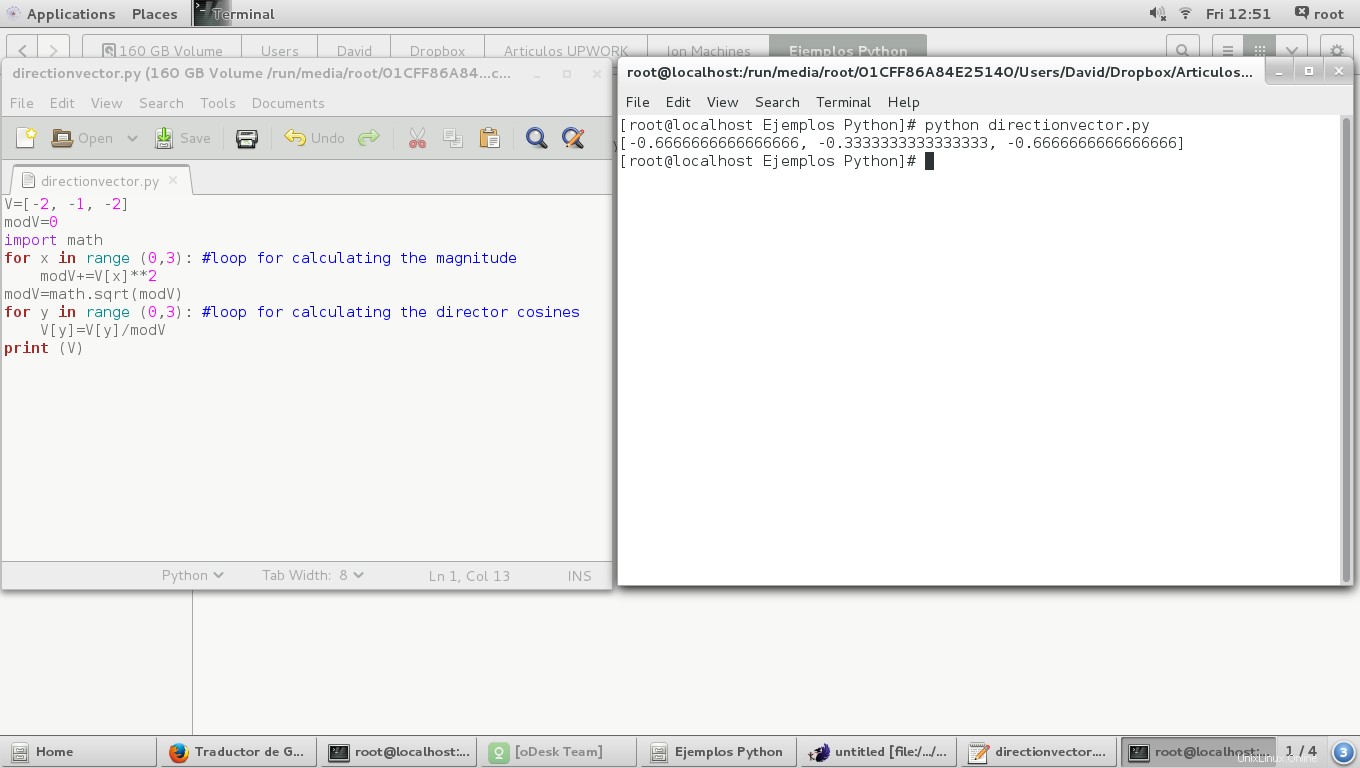
En la siguiente imagen podemos ver que los ángulos del director son diferentes en 180 grados de los originales
Suma algebraica vectorial
Primero tenemos que declarar todos los vectores involucrados en la suma algebraica, como es:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
donde vamos a sumar A más B y el resultado se almacenará en S
Agregar dos vectores (listas) en Python es equivalente a ejecutar un bucle 'for' para cada coordenada del vector resultante, por lo que tenemos que hacer lo siguiente:
for x in range(0,3):
S[x]=A[x]+B[x]
Aquí tenemos el script completo para la suma vectorial algebraica:
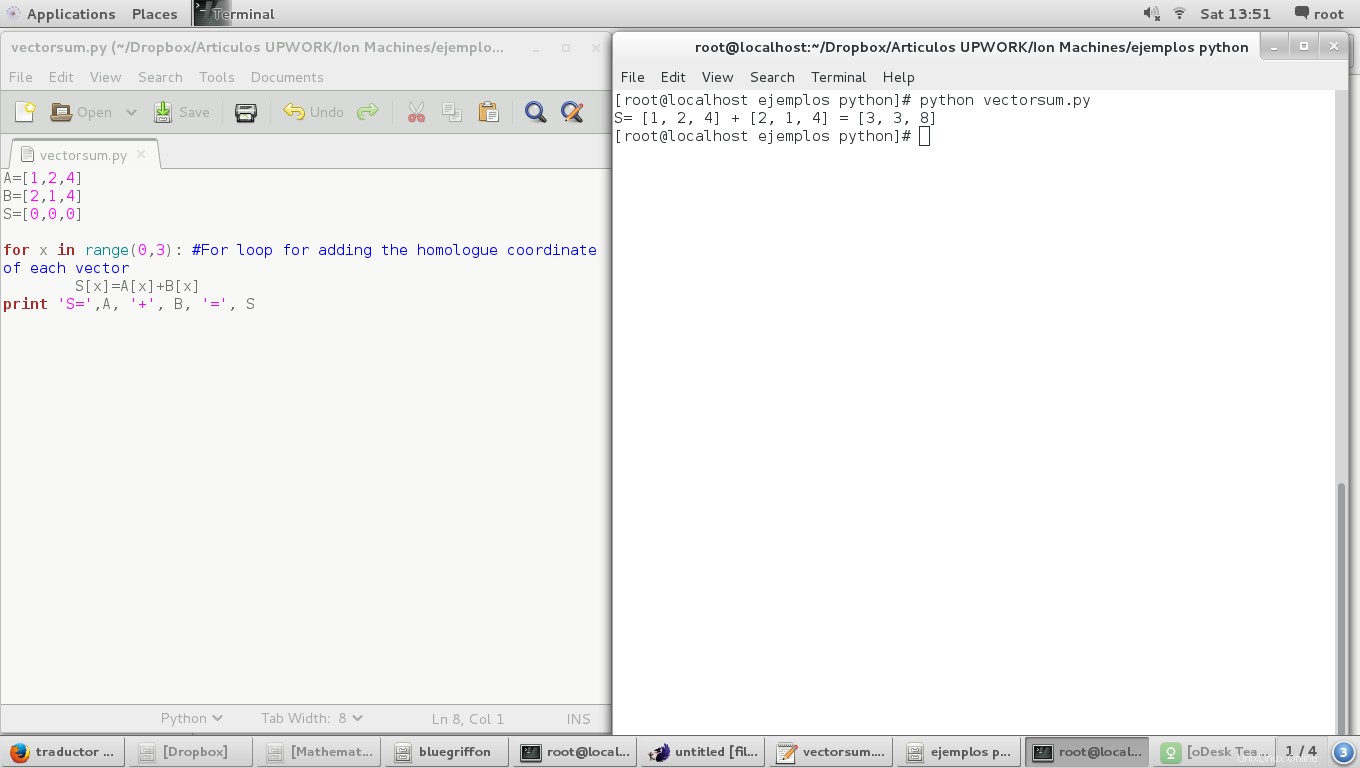
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
print 'S=',A, '+', B, '=', S
Y el resultado es:
Producto de un vector por un escalar
Dado un vector:
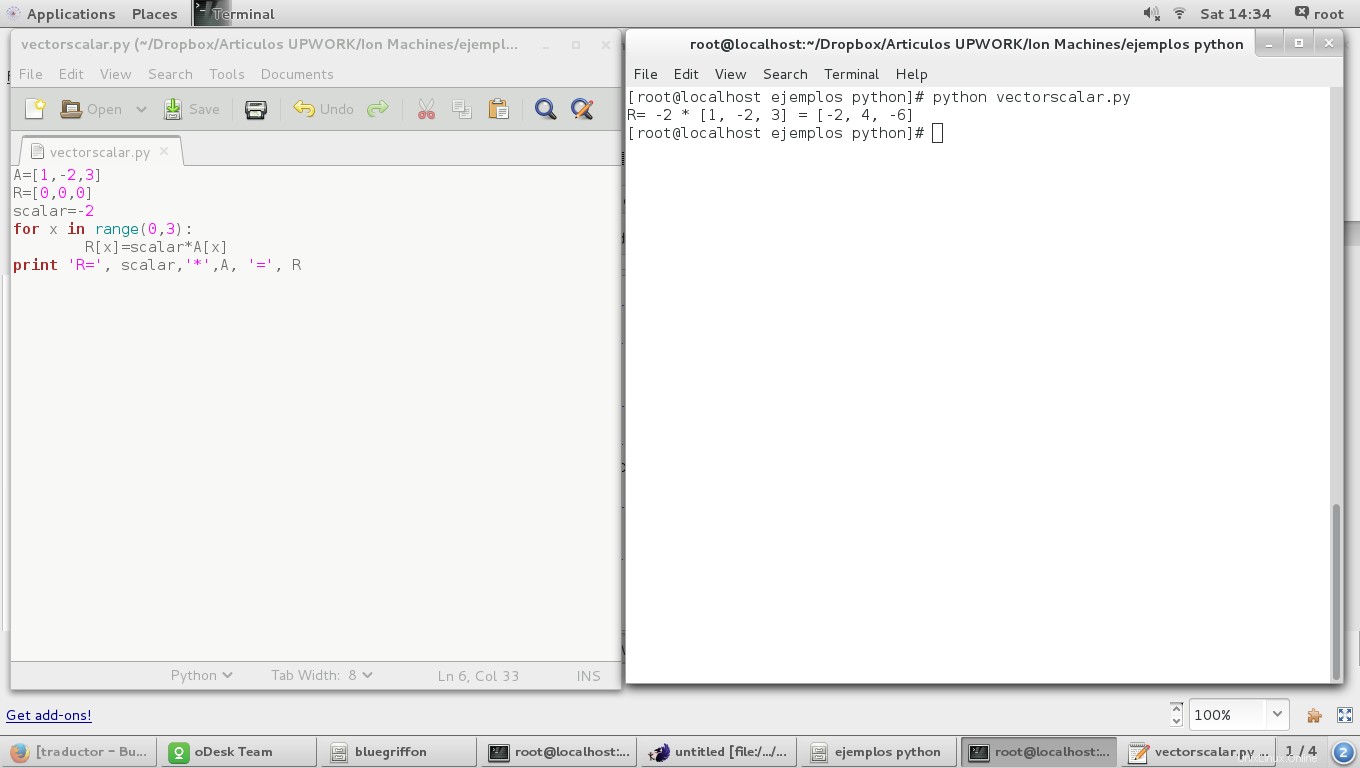
A=[1,-2,3]
y un escalar:
scalar=-2
producto vectorial por un escalar se define como el producto escalar de cada una de las coordenadas del vector:
for x in range(0,3):
R[x]=scalar*A[x]
y el resultado es:
Vector Unidad
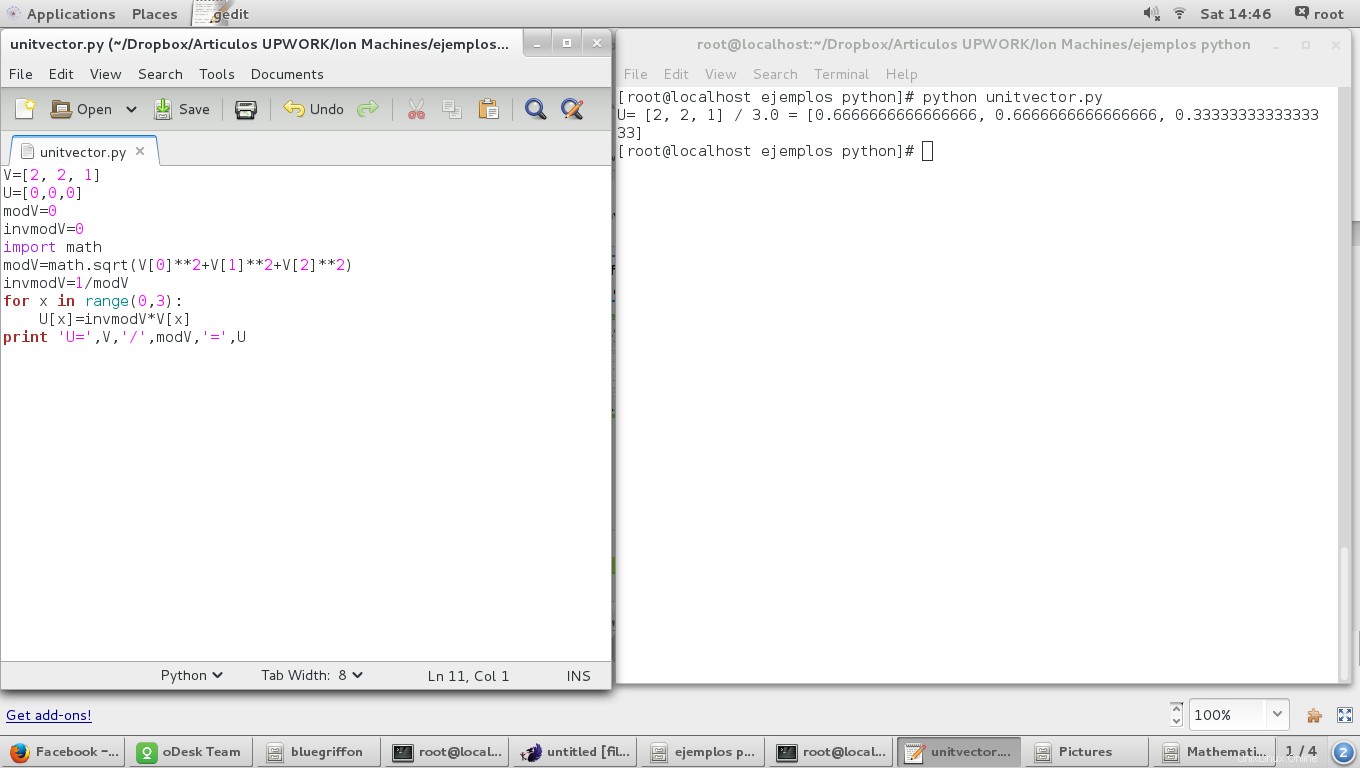
Usando el script 'Magnitud de un vector' tenemos:
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
print 'U=',V,'/',modV,'=',U
y el resultado es:
Combinación lineal
Dados tres vectores, A, B y C, podemos calcular los valores escalares que, multiplicados por B y C, respectivamente, dan como resultado el vector A. En otras palabras, colocar el vector A como una combinación lineal de los vectores B y C :
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]
Una combinación lineal da como resultado un sistema de ecuaciones, 3 ecuaciones con 2 variables (escalares) si son tres vectores en r3, o 2 ecuaciones con 2 variables si son dos vectores en R3, que se pueden resolver aplicando un determinante de una matriz. Aquí debemos hacer un punto debido a los tipos de datos que maneja Python. En muchos casos, al calcular los escalares involucrados en una combinación lineal, el resultado tendrá lugares decimales, lo que da como resultado operaciones de punto flotante. Los tipos de datos numéricos, manejados por Python, son:Integer, Real, Long. Entonces, tenemos que insertar las coordenadas de los vectores como datos de tipo Real, para que estos representen números reales (coma flotante). Debemos conocer y comprender algunas características del tipo de datos en Python:
- Entero ocupa menos espacio de memoria que el tipo Real.
- Las operaciones con Real son más lentas que con Integer.
Aquí tenemos los mismos vectores, pero declarados como de tipo Real:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
Entonces, con esto podemos intercambiar los vectores y así tener siempre la solución del sistema.
La primera verificación que tenemos que hacer es si hay o no coplanaridad entre los vectores, para así saber si hay o no es una combinación lineal. Para eso, vamos a implementar una matriz determinante:
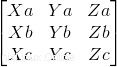
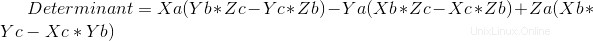
Código:
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
Si este determinante es igual a cero (0) entonces hay una dependencia lineal entre los vectores y podemos seguir calculando los escalares. Como se mencionó anteriormente, el sistema de ecuaciones tiene tres ecuaciones con dos variables, dando un determinado sistema compatible, para lo cual debemos tomar dos de las tres ecuaciones y resolver valores escalares, luego verificar con la tercera ecuación, no tomada antes, si la anterior los valores escalares lo resuelven. Si no resuelven esto, entonces no hay Combinación Lineal.
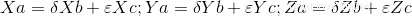
Aquí tenemos el código completo:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
Y el resultado:
[[email protected] ejemplos python]# python lincomb.py
Scalar 1 = 3.0 Scalar 2 = -2.0
[7.0, 9.0, -8.0] = 3.0 * [1.0, 3.0, -2.0] + -2.0 * [-2.0, 0.0, 1.0]
[[email protected] ejemplos python]#
En conclusión, el álgebra vectorial básica da como resultado una serie de operaciones que involucran sistemas lineales de ecuaciones y/o aritmética simple con números reales. En otro tutorial veremos cómo podemos desarrollar productos con vectores, como producto punto, producto cruzado o producto mixto.