Tutorial de Python SciPy:una guía para principiantes

Introducción

La informática es una parte esencial de la investigación científica. Los problemas matemáticos, de ingeniería, científicos y otros problemas técnicos son complejos y requieren potencia y velocidad informática. Python proporciona la biblioteca SciPy para resolver problemas técnicos computacionalmente.

Este artículo presenta un tutorial de SciPy y cómo implementar el código en Python con ejemplos.

Requisitos previos

• Python 2.7 o Python 3 instalado
• Un entorno de Python para ejecutar el código.
• Biblioteca SciPy instalada.
• Biblioteca NumPy instalada (Siga nuestra guía:Cómo instalar NumPy).
• Biblioteca Matplotlib instalada para trazado (opcional).

¿Qué es SciPy?

SciPy (Ciencia entífico Py thon) es un módulo de computación científica de código abierto para Python. Basado en NumPy, SciPy incluye herramientas para resolver problemas científicos. Los científicos crearon esta biblioteca para abordar sus crecientes necesidades para resolver problemas complejos.

SciPy contra NumPy

La biblioteca NumPy (Num Erica Py thon) hace cálculos numéricos. Los científicos usan esta biblioteca para trabajar con arreglos, ya que NumPy cubre usos elementales en ciencia de datos, estadísticas y matemáticas.

SciPy cubre funciones y cálculos avanzados. Esta biblioteca agrega más funciones de ciencia de datos, todas las funciones de álgebra lineal y algoritmos científicos estándar.

¿Por qué usar SciPy?

La biblioteca SciPy se basa en NumPy y funciona en matrices. El poder computacional es rápido porque NumPy usa C para la evaluación.

La pila científica de Python es similar a MATLAB, Octave, Scilab y Fortran. La principal diferencia es que Python es fácil de aprender y escribir.

Subpaquetes de SciPy

La biblioteca SciPy tiene diferentes grupos de subpaquetes. Hay dos formas de importar subpaquetes desde el módulo SciPy:

import scipy.<sub package name> as <alias>

O alternativamente:

from scipy import <sub package name> as <alias>

En ambos métodos de importación, el alias es opcional.

Funciones SciPy

SciPy incluye muchas de las funciones de matriz principal disponibles en NumPy y algunos de los módulos de uso común de los subpaquetes de SciPy.

Para importar una función desde un subpaquete, use:

from scipy.<subpackage> import <function>

Funciones básicas

Para obtener ayuda e información sobre cualquier función de SciPy, use help() comando:

help(<name of function>)

La help() El comando no necesita parámetros. Después de ejecutar sin parámetros, aparece un mensaje donde ingresa el nombre de la función.

Otra forma rápida de obtener ayuda con cualquier comando en Python es escribir el nombre del comando, colocar un signo de interrogación al final y ejecutar el código.

Funciones especiales

Las funciones especiales del módulo SciPy incluyen cálculos y algoritmos de uso común. Todas las funciones especiales aceptan matrices NumPy como entrada. Los cálculos son por elementos.

Para importar el special subpaquete, use:

import scipy.special as special

O alternativamente:

from scipy import special

Para importar una función específica desde el special subpaquete, use:

from scipy.special import <function name>

factoriales

Evalúa el factorial de cualquier número ejecutando:

special.factorial(<integer or array>)

Por ejemplo, para encontrar el factorial de diez, usa:

special.factorial(10)

Permutaciones y Combinaciones

Para encontrar el número de permutaciones, use:

special.perm(<number of elements>, <number of elements taken>)

Por ejemplo, para ver el número de permutaciones de tres elementos tomados de dos en dos:

special.perm(6,2)

Del mismo modo, encuentra el número de combinaciones con:

special.comb(<number of elements>, <number of elements taken>, repetition=<True or False>)

Para encontrar el número de combinaciones de tres elementos tomados de dos en dos con repetición, ingrese:

special.comb(6,2, repetition=True)

Las permutaciones y combinaciones se utilizan en los algoritmos de clasificación de las ciencias de la computación.

Funciones exponenciales

Las funciones exponenciales evalúan los exponentes para diferentes bases.

Calcula los exponentes en base diez con:

special.exp10(<integer or array>)

Por ejemplo:

special.exp10([0,1,2])

La informática a menudo usa funciones exponenciales de base dos:

special.exp2(<integer or array>)

Calcula la décima potencia de base dos con:

special.exp2(10)

Suma logarítmica de exponenciales

La suma logarítmica de exponenciales (LSE o LogSumExp) es una aproximación utilizada por los algoritmos de aprendizaje automático. Calcular el LSE con:

special.logsumexp(<integer or array>)

Función de Bessel

Las funciones de Bessel aparecen en problemas de propagación de ondas, procesamiento de señales y potencial estático. Encuentre la función de Bessel de primer tipo con:

special.jn(<integer order>, <integer or array>)

Aprovecha la pila completa para visualizar la función de Bessel. Para encontrar la función de Bessel de segundo orden del primer tipo, utilice:

#import stack
import scipy.special as special
import matplotlib.pyplot as plt
import numpy as np
#The X-axis
x = np.linspace(1,50,100)
#Bessel function of the first kind order two
jn1 = special.jn(2,x)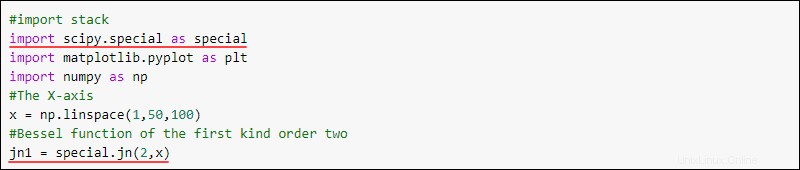

Trazar los resultados:

#Plotting
plt.title('Bessel function first kind order two')
plt.plot(x, jn1)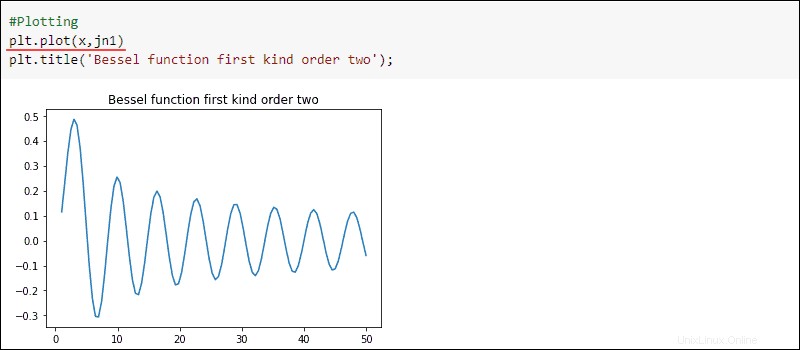

Funciones de Integración y ODE

SciPy proporciona un subpaquete para cálculos con integrales definidas. Para importar el integrate subpaquete, use:

import scipy.integrate as integrate

O alternativamente:

from scipy import integrate

Importe una función específica del subpaquete integrate con:

from scipy.integrate import <function name>

Integración general

Calcule una integral de una sola variable con el quad función de integrate subpaquete:

integrate.quad(<function>, <lower limit>, <upper limit>)

La function la entrada se define mediante una función lambda.

Por ejemplo, para calcular la integral definida de la función x+1 entre cero y uno:

from scipy import integrate
f = lambda x: x+1
integrate.quad(f, 0, 1)

La salida muestra dos valores. El primer valor es la integral evaluada, y el segundo es el error de estimación.

Funciones de optimización

SciPy tiene un subpaquete de optimización para encontrar el mínimo o el máximo de una función. optimize El subpaquete incluye solucionadores y algoritmos para encontrar valores óptimos locales y globales.

Para importar el subpaquete de optimización:

from scipy import optimize

O usa:

import scipy.optimize as optimize

Para importar una función específica del subpaquete optimize , ejecuta:

from scipy.optimize import <function name>

Minimizar una función

Encontrar un mínimo de una función se usa en el aprendizaje automático para reducir la pérdida (o error) de un algoritmo.

Por ejemplo, puede crear una función y encontrar el mínimo. Para hacerlo, utilice el fmin función de optimize subpaquete en SciPy:

#Import stack
import numpy as np
from scipy import optimize
#Defining inverse sine function
def f(x):
    return -np.sin(x)
#X-axis
x = np.linspace(0,5,100)
#Starting point
start = 3
#Simplex algorithm for optimization
optimized = optimize.fmin(f,start)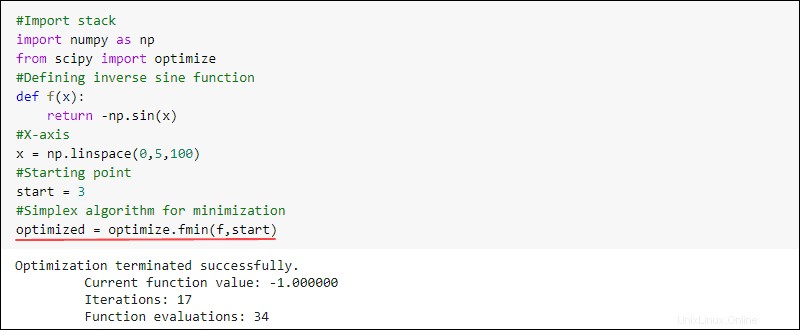

Para trazar el resultado, ejecute:

import matplotlib.pyplot as plt
plt.plot(x, f(x))
plt.scatter(start,f(start))
plt.scatter(optimized, f(optimized))
plt.legend(['Function -sin(x)', 'Starting point', 'Optimized minimum'])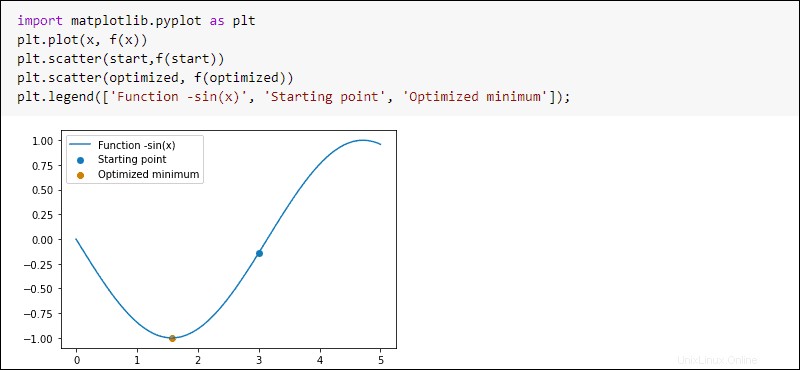

Funciones de Transformación de Fourier

SciPy incluye un subpaquete para funciones de transformación de Fourier llamado fftpack . Las transformaciones son Transformaciones Discretas de Fourier (DFT). Todas las transformaciones se aplican mediante el algoritmo de transformación rápida de Fourier (FFT).

Para importar el fftpack subpaquete, use:

import scipy.fftpack as fftpack

O:

from scipy import fftpack

Transformada rápida de Fourier

Como ejemplo, cree una función periódica como la suma de tres ondas sinusoidales:

import numpy as np
freq_samp = 100
#Time
t = np.linspace(0, 1, freq_samp*2, endpoint = False )
#Frequencies
f1, f2, f3 = 1, 5, 20
#Amplitudes
A1, A2, A3 = 3, 2, 1
x1 = A1*np.sin(f1*2*np.pi*t)
x2 = A2*np.sin(f2*2*np.pi*t)
x3 = A3*np.sin(f3*2*np.pi*t)
#Sum of waves
x = x1+x2+x3

Traza las ondas usando matplotlib :

import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(t,x1,t,x2,t,x3)
plt.subplot(2,1,2)
plt.plot(t,x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');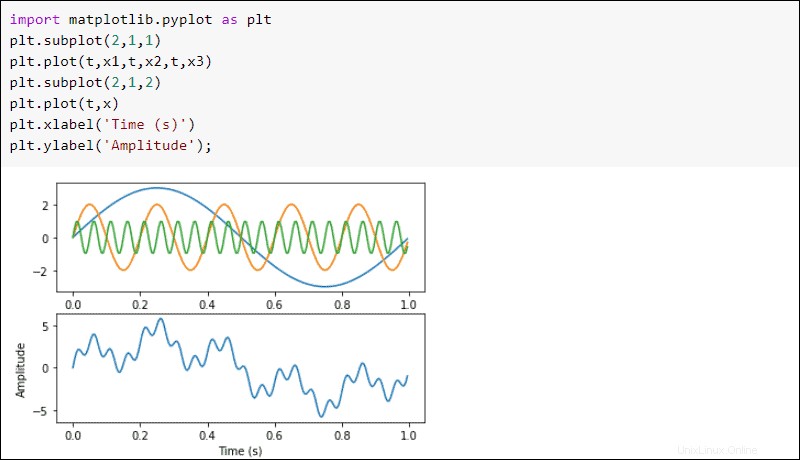

A continuación, aplique el fft y fftfreq funciones del fftpack para hacer una transformada de Fourier de la señal.

from scipy import fftpack
A = fftpack.fft(x)
freq = fftpack.fftfreq(len(x))*freq_samp*2

Grafique los resultados para ver el dominio de frecuencia:

plt.stem(freq,np.abs(A)/freq_samp,use_line_collection=True)
plt.xlim(-25,25)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()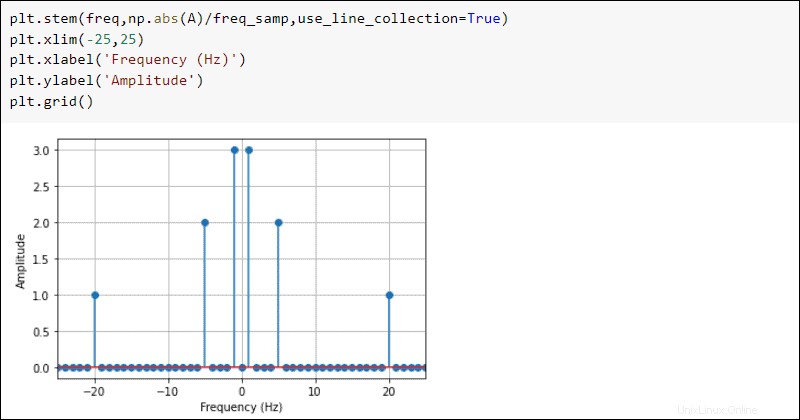

Funciones de procesamiento de señales

El subpaquete signal incluye funciones utilizadas en el procesamiento de señales. Para importar signal , ejecuta:

import scipy.signal as signal

O alternativamente:

from scipy import signal

Convolución

Una tarea común en el procesamiento de señales es la convolución. El subpaquete SciPy signal tiene la función convolve para realizar esta tarea. Por ejemplo, cree dos señales con diferentes frecuencias:

import numpy as np
#Time
t = np.linspace(0,1,100)
#Frequency
f1, f2 = 5, 2
#Two signals of different frequencies
first_signal = np.sin(f1*2*np.pi*t)
second_signal = np.sin(f2*2*np.pi*t)

Trazar las señales:

import matplotlib.pyplot as plt
#Plotting both signals
plt.subplot(2,1,1)
plt.plot(t, first_signal)
plt.subplot(2,1,2)
plt.plot(t, second_signal)
plt.ylabel('Amplitude')
plt.xlabel('Time (s)')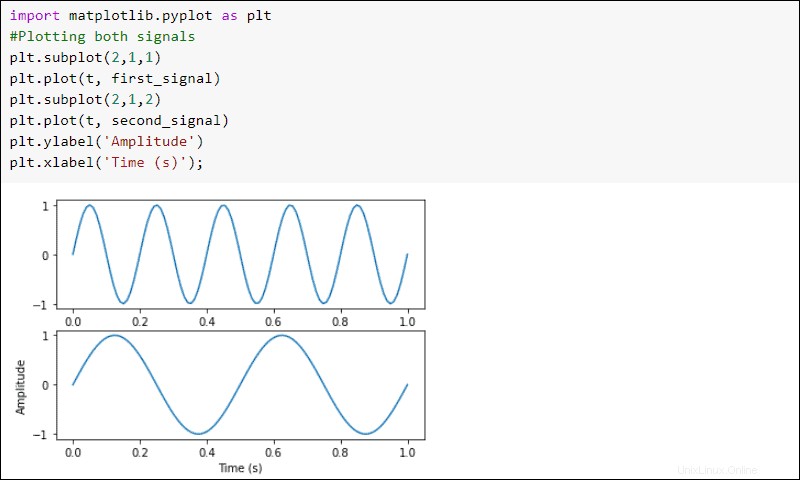

Importar la signal subpaquete de scipy . Usa el convolve función de la signal subpaquete para convolucionar las dos señales:

#Importing the signal subpackage
from scipy import signal
#Convolving two signals
convolution = signal.convolve(first_signal, second_signal, mode='same')

Trazar los resultados:

#Plotting the result
plt.plot(t, convolution)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')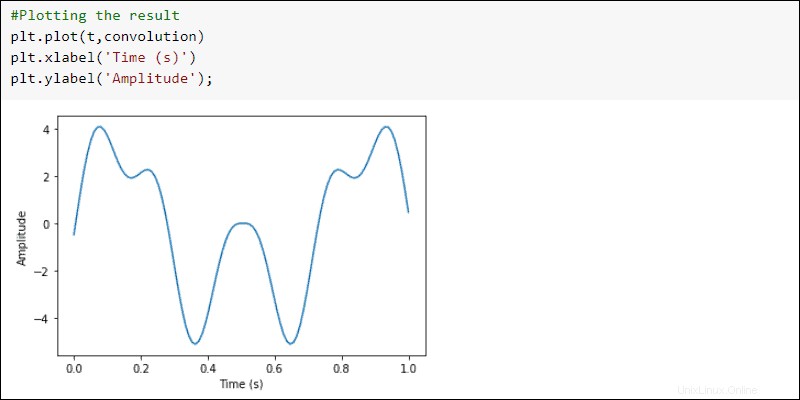

Funciones de interpolación

La interpolación se utiliza en el campo del análisis numérico para generalizar valores entre dos puntos. SciPy tiene la interpolate subpaquete con funciones de interpolación y algoritmos.

Importar el interpolate subpaquete con:

import scipy.interpolate as interpolate

O:

from scipy import interpolate

Interpolación unidimensional

La interpolate de SciPy subpaquete tiene el interp1d función para la interpolación unidimensional de datos. Como ejemplo, cree juguete datos usando numpy :

import numpy as np
#Create toy data
x = np.arange(0,10,0.5)
y = np.sin(x)

Interpolar los datos con interp1d de la interpolate subpaquete:

from scipy import interpolate
#Interpolate
f = interpolate.interp1d(x, y)
#Create interpolation function
x_i = np.arange(0,10,3)
y_i = f(x_i)

Trazar los resultados:

#Plot results
plt.scatter(x,y)
plt.plot(x_i, y_i)
plt.legend(['Interpolation', 'Data points'])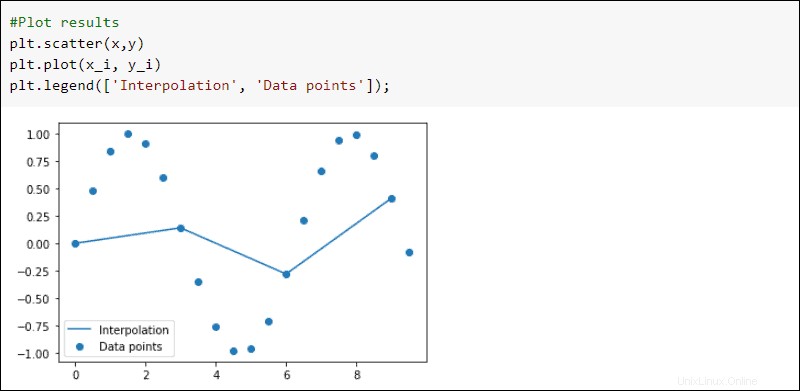

Álgebra lineal

SciPy tiene un subpaquete de álgebra lineal con todas las funciones. El subpaquete de álgebra lineal SciPy está optimizado con las bibliotecas ATLAS LAPACK y BLAS para un cálculo más rápido.

Para importar el paquete de álgebra lineal de SciPy, ejecute:

import scipy.linalg as linalg

O usa:

from scipy import linalg

Todas las funciones de álgebra lineal esperan una matriz NumPy para la entrada.

Determinante

Calcular el determinante de una matriz con det del linalg subpaquete:

linalg.det(<numpy array>)

Por ejemplo:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the determinant
linalg.det(A)

Matriz inversa

Determine la matriz inversa usando inv :

linalg.inv(<numpy array>)

Por ejemplo:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3,4]])
from scipy import linalg
#Calculate the inverse matrix
linalg.inv(A)

Vectores propios y valores propios

Los vectores propios y los valores propios son un método de descomposición de matrices. El problema de valores propios-vectores propios es un problema de álgebra lineal comúnmente implementado.

El eig función encuentra los valores propios y los vectores propios de una matriz:

linalg.eig(<numpy array>)

La salida devuelve dos matrices. El primero contiene valores propios y el segundo tiene vectores propios para la matriz dada. Por ejemplo:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the eigenvalues and eigenvectors
linalg.eig(A)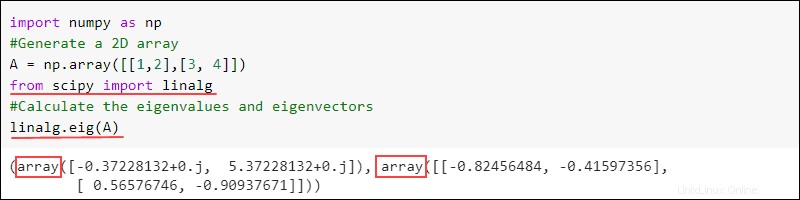

Estructuras de datos espaciales y algoritmos

Las estructuras de datos espaciales son objetos hechos de puntos, líneas y superficies. SciPy tiene algoritmos para estructuras de datos espaciales, ya que se aplican a muchas disciplinas científicas.

Importar el spatial subpaquete de SciPy con:

import scipy.spatial as spatial

O:

from scipy import spatial

Un ejemplo notable de un algoritmo espacial es el diagrama de Voronoi. Para un conjunto dado de puntos, los mapas de Voronoi dividen un plano en regiones. Si un nuevo punto cae en una región, el punto en la región es el vecino más cercano.

Como ejemplo, cree un diagrama de Voronoi a partir de veinte puntos aleatorios:

from scipy.spatial import Voronoi
import numpy as np
points = np.random.rand(20,2)
voronoi = Voronoi(points)
from scipy.spatial import voronoi_plot_2d
fig = voronoi_plot_2d(voronoi,show_vertices=False)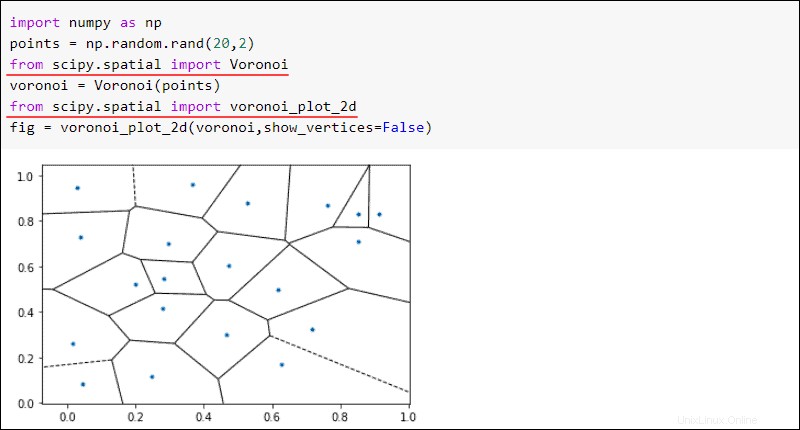

Procesamiento de imágenes

SciPy tiene un subpaquete para varios procesamientos de imágenes n-dimensionales. Para importar la ndimage subpaquete, ejecute:

import scipy.ndimage as ndimage

O usa:

from scipy import ndimage

El SciPy misc El subpaquete contiene una imagen de muestra para fines de demostración. Para importar el misc subpaquete y mostrar la imagen:

from scipy import misc
from matplotlib import pyplot as plt
raccoon = misc.face()
#show image
plt.imshow(raccoon)
plt.show()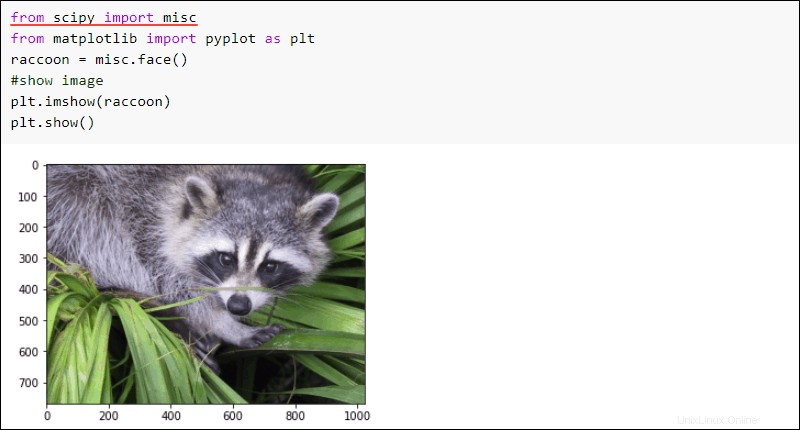

Importar la ndimage subpaquete y aplique un uniform_filter a la imagen Muestre la imagen para ver los resultados:

from scipy import ndimage
filtered = ndimage.uniform_filter(raccoon)
plt.imshow(filtered)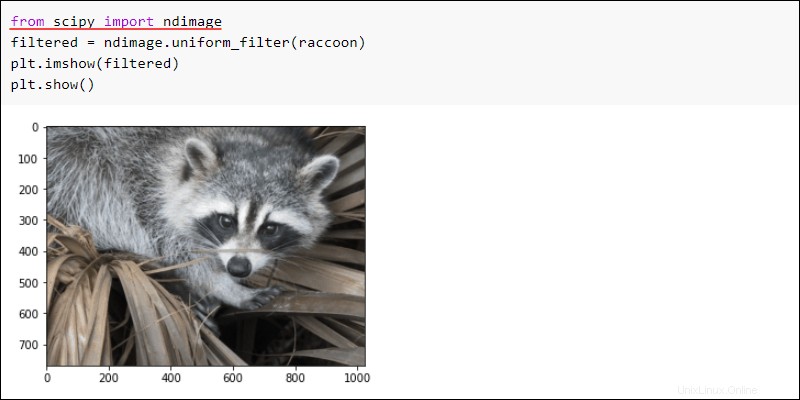

File IO (paquete de entrada/salida de archivos)

SciPy tiene un subpaquete de entrada y salida de archivos llamado io . El io El subpaquete se utiliza para leer y escribir formatos de datos de diferentes lenguajes y programas informáticos científicos, como Fortran, MATLAB, IDL, etc.

Importar el io subpaquete de SciPy con:

import scipy.io as sio

O usa:

from scipy import io as sio